#요인 늘려 기계학습 시키기
##공부시간(x1)만으로 성적을 예측해보았다면, 문제집 푼 개수(x2)의 요인을 추가하여 성적을 예측해보자.
from mpl_toolkits import mplot3d
x1=np.array([2,4,6,8]) #공부시간
x2=np.array([1,2,1,3]) #문제집 푼 개수
y=np.array([65,85,70,95])
ax=plt.axes(projection='3d')
ax.scatter(x1,x2,y)
plt.show()
#기계학습 시키기
import numpy as np
import matplotlib.pyplot as plt
x1=np.array([2,4,6,8]) #공부시간
x2=np.array([1,2,1,3]) #문제집 푼 개수
y=np.array([65,85,70,95])
a1=0
a2=0 #요인이 2개로 늘어나면서 기울기도 2개로 늘어남.
b=0
lr=0.005
for i in range(5000):
y_hat=a1*x1+a2*x2+b
error=y_hat-y #오차
a1_diff=sum(2*error*x1)
a2_diff=sum(2*error*x2)
b_diff=sum(2*error*1)
a1=a1-a1_diff*lr
a2=a2-a2_diff*lr
b=b-b_diff*lr
print(f'{i+1}회 학습 // 기울기1 {a1} //기울기2{a2}//절편 {b}')
plt.scatter(x1,y)
plt.plot(x1, a1*x1+a2*x2+b, 'r')
plt.show()

##요인이 2개로 늘어나면서 기울기 또한 2개로 늘어난다.
##요인이 1개일때는 일직선으로 그려지던 그래프가 2개로 늘어나면서 그래프가 더 정확하게 그려진다.
#어떠한 요인이 영향을 미치는지에 대해 파악하기
##데이터 가져오기
import pandas as pd
df=pd.read_csv("pima-indians-diabetes.csv",names=['pregnant','plasma','pressure','thickness','insulin','BMI',
'pedigree','age','class']) #열 이름 설정하기
df
##임신 횟수/혈당 농도/혈압/피부 주름 두께/인슐린/체질량지수/가족력/ 1=당뇨 ,0=당뇨 아니다
##데이터의 통계치 조회하기
df.describe()
##임신 횟수가 당뇨에 영향을 미치는지 알아보기
a=df.groupby('pregnant')['class'].mean()
a.plot()
##임신 횟수가 늘어날수록 당뇨수치 높아지는 것을 확인할 수 있다.
#히트맵을 통해 데이터들간의 상관관계 시각화하기
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10,10))
sns.heatmap(df.corr(),linecolor='white',annot=True) #annot에 True 값을 주면 실제값을 나타냄.
##대각선을 기준으로 그래프는 대칭을 이루고 있다.
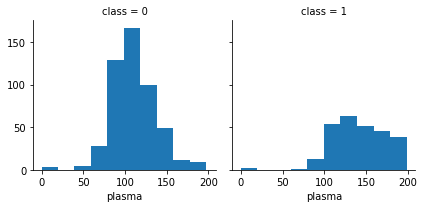
##당뇨별로 시각화하기
grid=sns.FacetGrid(df,col='class') #class 별로 나누는 함수
grid.map(plt.hist,'plasma',bins=10) #히스토그램
plt.show()
#K-최근접 이웃 분류 알고리즘(K-Nearest-Neighbors)이란?예측하려는 데이터 x가 주어졌을 때, 기존 데이터 중 가장 가까운 거리의 이웃 데이터 k개를 찾아, 이웃 데이터가 가장 많이 속해있는 데이터를 예측 값으로 결정하는 방법이다.

##위 그림에서 6개의 데이터를 이웃 데이터로 설정하여 최근접 이웃 분류를 한다고 했을 때,새로운 데이터에서 가장 가까운 6개의 데이터들 중 개수가 더 많은 초록 동그라미 데이터로 분류가 된다.
#k-최근접 이웃 분류를 이용한 도미,빙어 분류 머신러닝 만들기


##도미 데이터(길이, 무게) 저장하고 분산도로 나타내기
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
plt.scatter(bream_length,bream_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

##빙어 데이터(길이, 무게) 저장하고 분산도 나타내기
#빙어 데이터
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
plt.scatter(smelt_length,smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
##도미와 빙어 분산도 같이 나타내기
plt.scatter(bream_length,bream_weight)
plt.scatter(smelt_length,smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
##학습시킬 문제지와 정답지 만들기
##데이터를 학습시킬 때, 머신러닝이 요구하는 데이터 모양이 있다.
##문제지 : 2차원 넘파이 배열
##정답지 : 1차원 넘파이 배열
##도미와 빙어의 길이 데이터, 무게 데이터 같이 저장하기
length=bream_length+smelt_length
weight=bream_weight+smelt_weight
##합쳐진 데이터 조회하기
>print(length) #문제지
[25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
>print(weight) #문제지
[242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
##길이와 무게 데이터를 하나로 묶어 2차원 리스트 형식으로 저장하기
>fish_data=[]
>for i,j in zip(length,weight):
> fish_data.append([i,j])
>
>fish_data
[[25.4, 242.0],
[26.3, 290.0],
[26.5, 340.0],
[29.0, 363.0],
[29.0, 430.0]
....생략......
[12.4, 13.4],
[13.0, 12.2],
[14.3, 19.7],
[15.0, 19.9]]>>이런식으로 저장하면 문제지의 형태인 2차원 배열 형태로 저장이 된다.
ex)[[길이1,무게1],[길이2,무게2],,,,[길이n,무게n]]
##정답지 만들기
>fish_target=[1]*35+[0]*14 #도미는 35,빙어 14
>print(fish_target)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]>>도미=1, 빙어 =0
##머신러닝 라이브러리를 이용하여 학습시키기
>from sklearn.neighbors import KNeighborsClassifier
>
>kn=KNeighborsClassifier() #kn이란 변수는 클래스를 받았으니까 모든 라이브러리 사용가능
>kn.fit(fish_data,fish_target) #fit 이란 함수에 문제지와 답안지 넣어주기만 하면 알아서 학습
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform') #학습이 완료되었다는 의미>>fit 함수를 이용하여 문제지와 답안지를 넣어주면 알아서 학습
##모델 성능 평가하기
#이 모델이 얼마나 정확한깋 알아보기
kn.score(fish_data, fish_target)
1.0>>학습한 걸 넣었기 때문에 당연히 성능 만점(1.0)이 나온다.
##데이터 예측해보기
kn.predict([[30,600]]) #2차원 넘파이 배열로 넣기
array([1])>>길이=30,무게=600 이면 빙어일까 도미일까??도미(=1)
#컴퓨터가 모르는 데이터를 넣어도 잘 예측할 수 있을지 알아보기
##이웃 데이터 개수 바꿔서 학습시키기
kn49=KNeighborsClassifier(n_neighbors=49) #이웃 데이터 개수 49개로 바꾸기
kn49.fit(fish_data,fish_target)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=49, p=2,
weights='uniform')
##성능 평가하기
kn49.score(fish_data,fish_target)
0.7142857142857143>>성능 떨어진다. 왜??도미 데이터의 개수(35)가 빙어 데이터의 개수(15)보다 많기 때문에 빙어 데이터를 넣었을 때에도 개수가 더 많은 도미 데이터를 더 많은 이웃 데이터로 인지했을 가능성 있기 때문에 성능이 떨어진다.
##이웃 데이터 개수별 성능 알아보기
>kn=KNeighborsClassifier()
>kn.fit(fish_data,fish_target)
>
>for n in range(1,50): #개수를 올려가며 정확도 파악하기,18개 되니까 확률 떨어지기 시작..
> kn.n_neighbors=n
> score=kn.score(fish_data,fish_target)
> print(n,score)
1 1.0
2 1.0
3 1.0
4 1.0
5 1.0
6 1.0
7 1.0
8 1.0
9 1.0
10 1.0
11 1.0
12 1.0
13 1.0
14 1.0
15 1.0
16 1.0
17 1.0
18 0.9795918367346939
19 0.9795918367346939
20 0.9795918367346939
21 0.9795918367346939
22 0.9795918367346939
23 0.9795918367346939
24 0.9795918367346939
25 0.9795918367346939
26 0.9795918367346939
27 0.9795918367346939
28 0.9591836734693877
29 0.7142857142857143
30 0.7142857142857143
31 0.7142857142857143
32 0.7142857142857143
33 0.7142857142857143
34 0.7142857142857143
35 0.7142857142857143
36 0.7142857142857143
37 0.7142857142857143
38 0.7142857142857143
39 0.7142857142857143
40 0.7142857142857143
41 0.7142857142857143
42 0.7142857142857143
43 0.7142857142857143
44 0.7142857142857143
45 0.7142857142857143
46 0.7142857142857143
47 0.7142857142857143
48 0.7142857142857143
49 0.7142857142857143
##학습 데이터와 테스트 데이터 나누기
train_input=fish_data[:35]
train_target=fish_target[:35]
test_input=fish_data[35:]
test_target=fish_target[35:]>>35번째 데이터까지는 학습데이터로 지정하고 나머지는 테스트 데이터로 지정한다.
##데이터 학습시키기
kn=KNeighborsClassifier()
kn.fit(train_input,train_target)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
##성능 확인하기
>kn.score(test_input,test_target)
0.0>>0점 나옴. 35번까지의 데이터는 도미의 데이터만 있었기 때문에 도미 데이터로만 학습된 모델에 나머지 데이터인 빙어 데이터를 넣었을 때 당연히 맞출 수가 없다. 이 문제점 해결하기 위해서 데이터를 섞어줘야 한다.
##데이터 2차원 넘파이 배열로 만들기
import numpy as np
input_arr=np.array(fish_data)
target_arr=np.array(fish_target)
input_arr
array([[ 25.4, 242. ],
[ 26.3, 290. ],
[ 26.5, 340. ],
[ 29. , 363. ],
[ 29. , 430. ],
[ 29.7, 450. ],
......생략......
[ 12. , 9.8],
[ 12.2, 12.2],
[ 12.4, 13.4],
[ 13. , 12.2],
[ 14.3, 19.7],
[ 15. , 19.9]])
##데이터 섞기
index=np.arange(49) #arange함수 : 0~48 까지 1차원 넘파이 배열에 저장
index
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48])np.random.shuffle(index) #인덱스 랜덤하게 섞기
index
array([32, 28, 14, 5, 3, 38, 46, 26, 44, 17, 6, 23, 0, 12, 39, 13, 36,
24, 33, 45, 35, 43, 11, 2, 37, 19, 16, 25, 30, 7, 34, 48, 29, 1,
18, 8, 10, 47, 22, 31, 41, 20, 40, 4, 9, 27, 15, 21, 42])
##랜덤하게 섞인 인덱스를 이용하여 학습 데이터와 테스트 데이터 지정하기
train_input=input_arr[index[:35]]
train_target=target_arr[index[:35]]
test_input=input_arr[index[35:]]
test_target=target_arr[index[35:]]
##랜덤하게 지정된 학습데이터 조회하기
train_input
array([[ 39.5, 925. ],
[ 36. , 850. ],
[ 32. , 600. ],
[ 29.7, 450. ],
[ 29. , 363. ],
[ 11. , 9.7],
[ 13. , 12.2],
......생략......
[ 33. , 700. ],
[ 35. , 725. ],
[ 38.5, 920. ],
[ 30. , 390. ],
[ 41. , 950. ],
[ 15. , 19.9],
[ 37. , 1000. ],
[ 26.3, 290. ],
[ 33.5, 610. ]])
##랜덤하게 섞인 학습 데이터와 테스트 데이터의 분산도 나타내기
plt.scatter(train_input[:,0],train_input[:,1])
plt.scatter(test_input[:,0],test_input[:,1])
plt.show()
##데이터 학습시키기
>kn=KNeighborsClassifier()
>kn.fit(train_input,train_target)
kn=KNeighborsClassifier()
kn.fit(train_input,train_target)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
##성능 확인하기
>kn.score(test_input,test_target)
1.0>>전혀 보지 못한 데이터를 넣었음에도 만점이 나왔다.
##예측값 보기
kn.predict(test_input[:10])
array([1, 1, 0, 1, 1, 0, 1, 0, 1, 1])
##실제 정답 보기
test_target[:10]
array([1, 1, 0, 1, 1, 0, 1, 0, 1, 1])
##데이터 예측하기
>kn.predict([[25,150]])
array([0])
##도미와 빙어 데이터 산점도와 예측 데이터 산점도에 나타내기
plt.scatter(train_input[:,0],train_input[:,1])
plt.scatter(25,150,marker='^')
plt.show()
##예측 데이터에서 가장 가까운 5개 데이터 거리와 인덱스 출력하기
>distances,indexes=kn.kneighbors([[25,150]])
>print(distances,indexes)
[[ 92.00086956 130.48375378 137.17988191 138.32150953 138.39320793]] [[12 31 19 6 8]]
##가장 가까운 5개의 데이터 산점도에서 나타내기
plt.scatter(train_input[:,0],train_input[:,1])
plt.scatter(25,150,marker='^')
plt.scatter(train_input[indexes,0],train_input[indexes,1],marker='D')
plt.show()
>>여기서 문제점은 x축과 y축의 단위의 차이가 크다는 점! x축은 5씩, y축은 200씩 증가
컴퓨터가 학습할 때는 수치가 큰 것을 더 중요한 데이터라고 인식하지만 둘 다 중요한 데이터임을 알려줘야 한다.
##정규분포 이용하여 데이터 중요도의 평등성 만들기
mean=np.mean(train_input,axis=0) #평균
std=np.std(train_input,axis=0) #표준편차
##평균과 표준편차 출력하기
>mean #길이의 평균, 무게의 평균
array([ 27.05142857, 449.37714286])
>std #길이의 표준편차, 무게의 표준펀차
array([ 10.32462719, 336.04098312])
##데이터 정규화 하기
>train_scaled=(train_input-mean)/std
>test_scaled=(test_input-mean)/std
>train_scaled
array([[ 1.20571631, 1.41537158],
[ 0.86672102, 1.19218452],
[ 0.47929783, 0.44822764],
[ 0.2565295 , 0.00185352],
[ 0.18873044, -0.25704348],
[-1.55467392, -1.30840333],
..........생략.............
[ 1.10886052, 1.40049244],
[ 0.28558624, -0.17669613],
[ 1.35100001, 1.48976727],
[-1.16725073, -1.27804989],
[ 0.96357682, 1.63855864],
[-0.07278021, -0.47427889],
[ 0.62458153, 0.47798592]])
##예측값 정규화 및 산점도에 전체 데이터 나타내기
new=([25,150]-mean)/std
plt.scatter(train_scaled[:,0],train_scaled[:,1])
plt.scatter(new[0],new[1],marker='^')
plt.show()
>>축이 일정해진 것을 확인할 수 있다.
##정규화된 데이터 학습시키기
>kn=KNeighborsClassifier()
>kn.fit(train_scaled,train_target)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
##성능 평가하기
kn.score(test_scaled,test_target)
1.0
##예측하기
kn.predict([new])
array([1])
##정규화된 데이터와 예측값 산점도에 나타내고 이웃 데이터 5개 나타내기
new=([25,150]-mean)/std
distances,indexes=kn.kneighbors([new])
plt.scatter(train_scaled[:,0],train_scaled[:,1])
plt.scatter(new[0],new[1],marker='^')
plt.scatter(train_scaled[indexes,0],train_scaled[indexes,1],marker='D')
plt.show()
'Python > 파이썬으로 배우는 머신러닝 기초 교육' 카테고리의 다른 글
| 6일차(선형 회귀와 로지스틱 회귀) (0) | 2021.08.11 |
|---|---|
| 5일차(K-최근접 이웃 회귀 모델) (0) | 2021.08.09 |
| 4일차(머신러닝 기초) (0) | 2021.07.28 |
| 4일차(데이터 분석 및 텍스트마이닝) (2) | 2021.07.27 |
| 3일차(데이터 분석 및 시각화) (0) | 2021.07.25 |
